Let's build a Bloom filter. Part 1 - A Space-Efficient Hash Set
I have always been intrigued by Bloom filters. They are very similar to hash sets but somehow consume much less memory. Sometimes, they can yield false positives, creating a peculiar tradeoff.
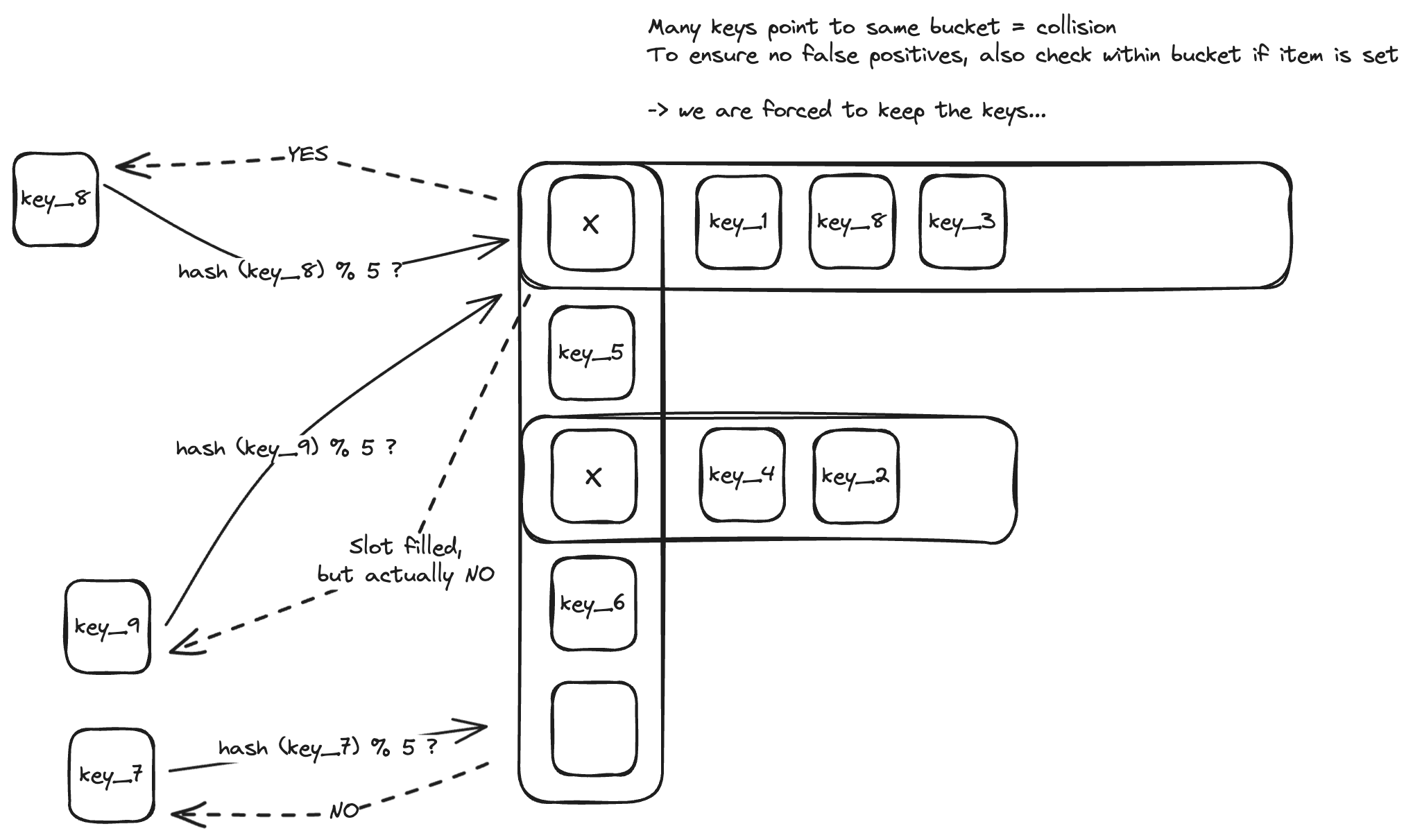
Let’s explore what makes Bloom filters tick, starting with a high-level comparison to a hash set. As a reminder, a hash set stores unique elements without any associated values. This allows only to check whether an item has been inserted within it or not. Similarly, Bloom filters are used solely for membership queries.
So, how much space we can actually save?
-
Hash set: Requires
4 bytes * Nfor 32-bit keys, such as integers. -
Bloom filter: Utilizes
(m (filter size in bits) / 8 bits) * Nbytes, as it doesn’t store the keys.
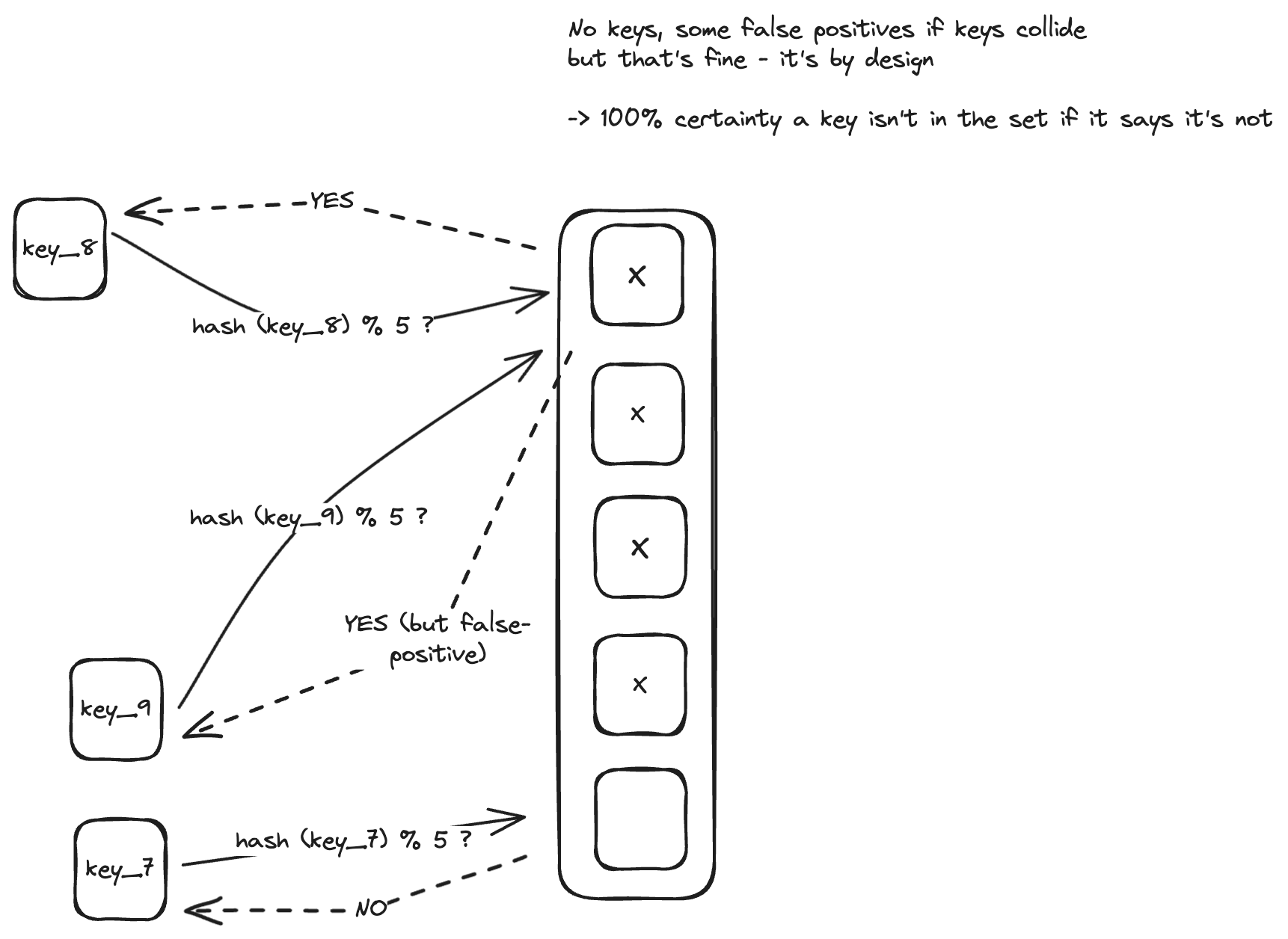
In practice, m is often set to be 20 times the element count. For a false positive rate (FP_rate) of 0.0001, we can save anywhere from 37% (using 32-bit ints) to 75% (with 10-character string keys). Excellent! The catch here is, once again (crucial to grasp) - Bloom filters do not store keys, so, unlike for hash sets, collisions are acceptable, and there’s no need to look up within the buckets.
How do we control FP rate?
To control the false positive rate, one can increase the value of ‘m.’ In practice as well, Bloom filters employ multiple hash functions when hashing keys to ensure better uniformity.
Let’s gain a better understanding of Bloom filters by implementing one, naturally, in Rust 🦀:
use sha2::{Sha256, Digest};
struct BloomFilter {
state: u8,
}
impl BloomFilter {
fn get_bucket(val: &str) -> u8 {
let mut hasher = Sha256::new();
hasher.update(val);
let hash = hasher.finalize();
let mut hash_int: u128 = 0;
for i in 0..16 {
hash_int = (hash_int << 8) + hash[i] as u128;
}
let bucket = hash_int % 8;
return bucket as u8;
}
fn new() -> Self {
BloomFilter {
state: 0
}
}
fn insert(&mut self, val: &str) {
let bucket = BloomFilter::get_bucket(val);
// getting the right bit
// duplication
let mut mask: u8 = 1;
for i in 0..bucket {
mask = mask << 1;
}
self.state = self.state | mask;
}
fn get(&self, val: &str) -> bool {
let bucket = BloomFilter::get_bucket(val);
// getting the right bit
let mut mask: u8 = 1;
for i in 0..bucket {
mask = mask << 1;
}
// e.g. only if all same bits are set in the mask (checking), then it means value
// has been set
return (mask & self.state) == mask
}
}
fn main() {
let mut bloom_filter = BloomFilter::new();
bloom_filter.insert("bla_bla");
println!("{}", bloom_filter.get("bla_bla"));
// so if it says false, then it means 100% it's not in the set. true means it might be there, but not guaranteed.
println!("{}", bloom_filter.get("bla_bla_6"));
}
struct BloomFilter {
state: u8,
}
Our filter relies on bit-backed buckets, a departure from hash sets using an array for buckets (since keys are not persisted). We use bits to indicate whether a bucket holds an element. The 8-bit limit in the code above simplifies the initial implementation, addressing challenges in directly manipulating bits on most architectures. Constructing a bitset from smaller memory units is a significant hassle.
Also, if you zoom in on the insert and get methods, you will notice that to get/set individual bits, we need to perform bit shift operations. This is because, once again, the smallest memory unit is a byte, and we cannot address individual bits directly.
fn main() {
let mut bloom_filter = BloomFilter::new();
bloom_filter.insert("bla_bla");
println!("{}", bloom_filter.get("bla_bla"));
// so if it says false, then it means 100% it's not in the set. true means it might be there, but not guaranteed.
println!("{}", bloom_filter.get("bla_bla_6"));
}
If you run the code above, you will likely get true and false. If you change values, you might notice that quite often the filter says a value exists, whereas we never actually added it. To address this, in the next chapter, we will attempt to reduce the false-positive rate by manipulating the Bloom filter’s size (m) and introducing additional hash functions to increase the uniformity of the value set (k).
Feel free to experiment with the implementation in the workspace below.
Full source is available on Github. Join the discussion on Hacker News.